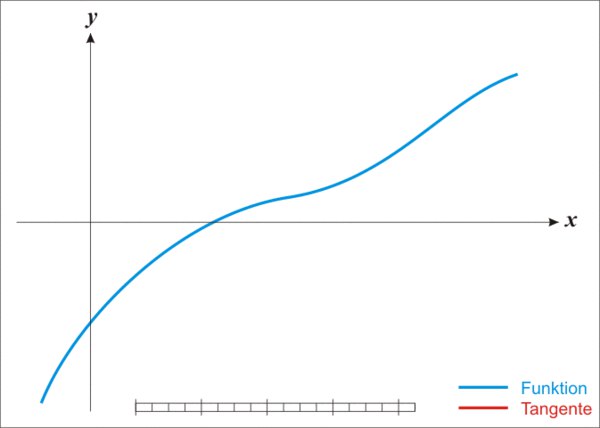
Given an input number ( m ), the goal is to find a value ( x ) such that ( x^2 = m ). Let ( f(x) = x^2 - m ), so the problem reduces to finding the root of the equation ( f(x) = 0 ). The derivative of ( f(x) ) is ( f’(x) = 2x ).
For a quadratic function, the derivative calculation is straightforward. The tangent line equation is ( y = f’(x_n)(x - x_n) + f(x_n) ), and finding the intersection point involves setting ( y ) to zero.
1package main
2
3import (
4 "fmt"
5 "math"
6)
7
8const err float64 = 1e-8 // err is the allowable error
9
10func Sqrt(x float64) float64 {
11 if x < 0 {
12 return -1
13 }
14 root := 1.0
15 for math.Abs(x - root * root) >= err {
16 root -= (root * root - x) / (2 * root)
17 }
18 return root
19}
20
21func main() {
22 fmt.Println(Sqrt(2))
23}